
Wissenschaftliches Praktikum

Mein Name ist Sebastian und ich bin Schüler der Internatsschule Schloss Hansenberg. Diesen Sommer werde ich dort das hessische Landesabitur ablegen. Nachdem die schriftlichen Prüfungen geschrieben sind, findet an unserer Schule bis zu den mündlichen Prüfungen kein Unterricht statt. In dieser Zeit wird uns die Chance geboten, uns in verschiedene Projekte zu vertiefen. Da ich mit dem Gedanken Mathematik zu studieren spiele, ergab sich das Praktikum am IWR als eine Chance zur Studienorientierung sowie um etwas über den schulischen Lehrplan hinaus zu lernen.
Während der Woche die ich in Heidelberg verbringe, wohne ich in der Jugendherberge. Diese liegt direkt am Universitätskampus und ist leicht von Innenstadt erreichbar.
Im Folgenden möchte ich einige Themen anstoßen, mit denen ich mich in meiner Zeit am IWR beschäftigt habe, damit Ihr einen Eindruck von meinem Praktikum erhaltet. Vielleicht wecken sie Euer Interesse.
Interpolation
Bei einer geringen Anzahl an Stützwerten ist jedoch der Fehler verhältnismäßig hoch. Daher wird versucht die einzelnen Punkte mit einer “Geschwungenen Linie” zu verbinden und deren Integral zu berechnen. Dabei wird für die (n+1) Stützpunkte ein Polynom des n-ten Grads gesucht, dass durch alle Punkte verläuft. Für die diskreten Daten wird eine stetige Funktion ermittelt, die diese Daten abbildet. Dieses Verfahren wird Interpolation genannt.
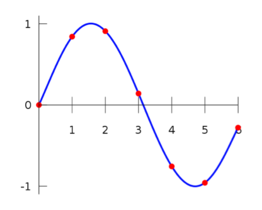
Grundlage des Verfahrens ist ein Gleichungssystem. Dabei werden die Daten in ein allgemeines Polynom mit entsprechenden Grad eingesetzt.
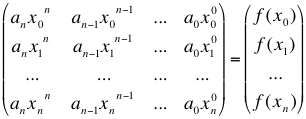
Interpolation mit Lagrangepolynomen
Das Lösen dieses Gleichungssystems ist jedoch bei größeren Messreihen mit einem erheblichen Rechenaufwand verbunden. Deswegen wird häufig die „Lagrange Interpolationsformel“ verwendet, mit der ich mich während meines Praktikums auseinandergesetzt habe. Mit ihr können auch die Gewichte der Keppl'rschen-Fassregel belegt werden.
Notwendige Bedingung für dieses verfahren ist die eindeutige Lösbarkeit des Gleichungssystems. Diese wird allgemein bei der Polynominterpolation erfüllt, weshalb die Formel verwendet werden kann. Dabei ist die fertige Annäherung p(x) die Summe der einzelnen Basisfunktionen.
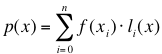
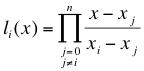
Entscheidend für diese Formel ist das die einzelnen „Lagrange-Basisfunktionen“ an einer Stützstelle den Wert 1 und an allen anderen den Wert 0 besitzen.
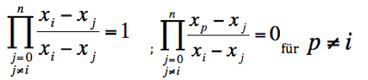
Durch Multiplikation der Basisfunktionen li(x) mit dem Funktionswert an der Stelle f(xi) besitzt sie an dieser Stelle den gegebenen Wert und beträgt an allen anderen Stützstellen 0. Durch Multiplizieren der Basisfunktionen mit dem Wert und Aufsummieren ergibt sich ein Polynom, das alle Stützstellen beinhaltet. Um den Flächeninhalt zu erhalten, kann das aus den Daten berechnete Polynom auf herkömmlichen Weg integriert werden.
Resumee
Neben dieser Hauptaufgabe konnte ich mich ebenfalls mit der Gruppentheorie und ihrer Anwendung zum Lösen von Gleichungssystemen beschäftigen. Zudem hatte ich die Gelegenheit trotz des kurzen Aufenthalts verschiedene Vorlesungen zu besuchen. Gerade für die Studienorientierung war dies eine prägende Erfahrung. Besonders im Vergleich zum Studium an anderen Universitäten fielen direkt die kleinen Hörsaale und geringe Anzahl an Studenten auf. Mich persönlich hat das Praktikum in meinem Studienwunsch bestätigt und mir sehr interessante Einblicke geboten. Daher kann ich es jedem, der sich bezüglich eines Mathematikstudiums unsicher ist oder einfach etwas in diesem Bereich dazulernen möchte, nur nahelegen sich für ein wissenschaftliches Praktikum am IWR zu bewerben.