Mein Praktikum am IWR
Hallo,
ich heiße Amrei und gehe in die 10. Klasse des Hölderlin Gymnasiums Heidelberg. Auf das IWR bin ich bei der Suche nach einem BOGY-Platz gestoßen. Das ist ein 1-wöchiges Praktikum, dass man in der 10.Klasse absolvieren muss. Ich habe mich dann schließlich dafür entschieden das BOGY am IWR zu machen, da ich mich für Mathe und Informatik interessiere. Während meines Praktikums habe ich das Thema „Aussagenlogik“ zugewiesen bekommen, über das ich mich dann genauer informiert habe.
Im Folgenden werde euch mehr über den Ablauf meines Praktikums erzählen.
Organisation einer Universität
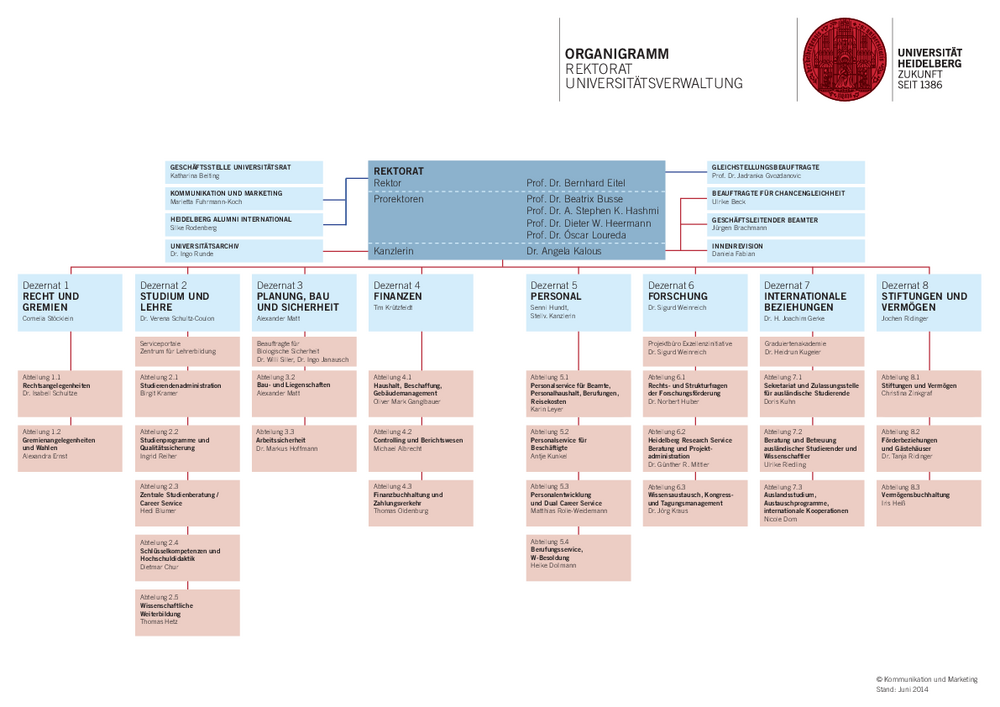
Bevor ich am ersten Tag mit der Recherche für mein Thema beginnen konnte, hatte ich noch eine Besprechung mit Herrn Winckler zu meinem Praktikum. Dort wurde mir neben der Bekanntgabe meines Themas, auch viel über die Uni und das IWR erzählt. Eine Universität hat demnach ähnlich wie in einer Schule oder in einem Staat einen bestimmten Aufbau. Dieser Aufbau ist in einem Organigramm genauer beschrieben. Zuerst einmal gibt es das Rektorat. Das besteht aus einem Rektor, 4 Prorektoren und einer Kanzlerin. Der Rektor wird für 6 Jahre von dem Universitätsrat, bestehend aus 6 externen und 6 internen Mitgliedern, gewählt und dann von einem Senat (darüber erzähle ich gleich noch etwas) in seinem Amt bestätigt. Zurzeit hat Prof. Dr. Bernhard Eitel dieses Amt inne. Die vier Prorektoren sind jeweils für einen der Geschäftsbereich Forschung & Transfer, Studium & Lehre, Internationale Angelegenheiten und Qualitätsentwicklung tätig. Die Prorektoren werden von dem Rektor vorgeschlagen und von dem oben erwähnten Senat gewählt. Das letzte Mitglied des Rektorats ist die Kanzlerin. Sie ist für den Haushalt der Universität zuständig und momentan ist Dr. Angela Kalous in diesem Amt. Nun zum Senat, er besteht aus dem Rektorat, den Dekanen aller zwölf Fakultäten, der Gleichstellungsbeauftragten der Uni und 20 gewählten Mitgliedern. Die Studienfächer der Universitäten sind nach sogenannten Fakultäten aufgeteilt. In der Universität Heidelberg gibt es insgesamt 12 dieser Fakultäten. Die Fakultäten werden immer von einem Dekan vertreten.
Das IWR
Nun zum IWR. Das IWR (Interdisziplinären Zentrums für Wissenschaftliches Rechnen) ist eine Zentrale wissenschaftliche Einrichtungen der Uni Heidelberg, was bedeutet, dass sie rechtlich unselbständig ist. Das IWR wurde 1987 gegründet und besteht aus 14 Professoren, 2 Juniorprofessoren und 35 weiteren Mitglieder. Anders als in der Universität, in der der Fokus hauptsächlich auf der Lehre liegt, dreht sich im IWR fast alles um die Forschung.
Mein Thema: Die Aussagenlogik
Am Dienstag habe ich dann vor allem an meinem Thema der Aussagenlogik recherchiert. Bevor ich beginne, möchte ich allerdings klären, was die Grundbegriffe des zusammengesetzten Wortes bedeuten.
Was ist logisch?
Das Wort Logik stammt von dem altgriechischen Wort logiké téchnē ab‚ was so viel bedeutet wie “denkende Kunst” oder “Vorgehensweise”. Wir sprechen von etwas logischem, wenn es sich in einzelnen Schritten vernünftig begründen lässt.
Was ist eine Aussage?
Bei einer Aussage (Proposition) handelt es sich um einen Satz den man einen der beiden Wahrheitswert also “wahr” oder “falsch” zuordnen kann. Bespiele für solche Aussagen sind:
1. heute ist es warm
2. heute ist es kalt
Die Aussagenlogik befasst sich mit der Verknüpfung einzelner Aussagen durch sogenannte Logische Operatoren und dem daraus resultierenden Wahrheitswert. Mit dem Beispiel von oben könnte das dann so aussehen:
Es ist heute kalt und warm
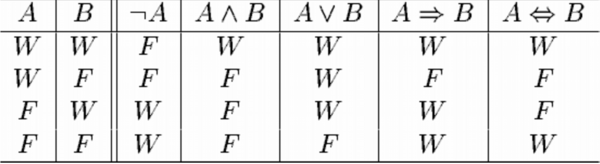
Die Frage ist nun, ob die gesamte Aussage nun falsch oder wahr ist. Wir haben den Operator “und” (^, Konjunktion) benutzt. Die Aussagen A^B sind nur dann wahr, wenn die Teilaussagen A und B wahr sind. Ist eine oder beide, wie in unserem Fall oben, falsch, ist die Gesamtaussage A^B falsch.
Bei dem Operator “oder” (∨, Disjunktion) ist das anders. Wenn mindestens eine der Aussagen A und B wahr ist, so ist A∨B auch wahr.
Dann gibt es auch noch das “nicht” (¬, Negation). Die Aussage ¬A besitzt dort immer dann den Wahrheitswert falsch, wenn die ursprünglich Aussage A den Wahrheitswert wahr besitzt und umgekehrt. ¬A ist also quasi das Spiegelbild von A.
Zuletzt gibt es noch die Äquivalenz (↔) und die Implikation (→). Die Äquivalenz von A zu B ist genau dann wahr, wenn beide den gleichen Wahrheitswert besitzen. Anders die Implikation (wenn...dann…), die nur dann den Wahrheitswert falsch annimmt, wenn A wahr und B falsch ist.
In der Tabelle oben (einer sogenannten Wahrheitstabelle), kann man sich noch einmal die Wahrheitswerte bei einzelnen Verknüpfungen anschauen.
In der Aussagenlogik gelten natürlich auch bestimmte Rechenregeln. Neben den bekannten Gesetzten dem Assoziativgesetz, dem Kommutativgesetz und dem Distributivgesetz, gibt es so auch die Morganischen Gesetze. Sie besagen, dass:
1. ¬(A∨B) ↔ ¬A∧¬B
2. ¬(A∧B) ↔ ¬A∨¬B
Doch wieso gelten diese beiden Gesetze. Hierfür ein kurzer Beweis für das Erste der Beiden:
Wenn ¬(A∨B) äquivalent zu ¬A∧¬B ist, dann gibt es einen Wahrheitswert c, der ebenfalls äquivalent zu ¬(A∨B) und ¬A∧¬B ist. Das bedeutet dann ausgeschrieben:
¬(A∨B) ↔ ¬A∧¬B ↔c
Wir gehen jetzt anfangs davon aus, dass c den Wahrheitswert wahr besitzt. Wenn also c ↔¬(A∨B) und c wahr ist, dann gilt auch, c ist nicht äquivalent zu A∨B und das bedeutet, dass der Ausdruck A∨B den Wahrheitswert falsch annehmen muss. Daraus folgt dann in Berücksichtigung einer Wahrheitstabelle, dass A und B beide auch den Wahrheitswert falsch haben müssen. c ist demnach äquivalent zu ¬A und ¬B:
c ↔ ¬A ↔ ¬B
Wenn ¬A und ¬B, beide den Wahrheitswert wahr besitzen, so ist die Formel ¬A∧¬B auch wahr. Daraus folgt dann:
¬(A∨B) ↔ ¬A∧¬B
Doch was ist, wenn c den Wahrheitswert falsch annimmt. Demnach wäre die Aussage ¬A∧¬B, da sie äquivalent zu c ist, auch falsch. Das geht mit Hinblick auf die Wertetabelle nur, wenn min. einer der beiden Ausdrücke ¬A oder ¬B ebenfalls den Wahrheitswert falsch annimmt. Wenn nun min. einer der beiden Ausdrücke ¬A oder ¬B den Wahrheitswerte falsch annimmt, bedeutet das, dass auch min. einer der beiden Aussagen A und B den Wahrheitswert wahr besitzt. Die Aussage ¬(A∨B) ist demnach falsch und es gilt wieder:
¬(A∨B) ↔ ¬A∧¬B
Tautologien:
Ist eine solche Formel immer wahr unabhängig von dem Wahrheitswert ihrer Aussagen, so spricht man von einer Tautologie. Ein Beispiel für eine Tautologie ist A∨(¬A). Die Morganische Regel ist übrigens auch eine Tautologie.
Gruppen
Am Mittwoch hatte ich dann nach eigenen Recherchen noch ein Gespräch mit Herrn Winckler. Das Thema waren Gruppen. Man bezeichnet eine Menge immer dann als eine Gruppe, wenn sie eine bestimmte Verknüpfung (°) besitzt und folgende Axiome erfüllt:
1. Es gibt in der Gruppe ein neutrales Element e. Das heißt, dass e verknüpft mit einem beliebigen
Element x der Gruppe, wieder x ergibt:
x°e=x
2. Zu jedem Element x der Gruppe gibt es ein anders sogenanntes inverses Element x‘ in der Gruppe, für
das gilt:
x°x‘=e
3. Des Weiteren gilt bei der Verknüpfung das Assoziativgesetz. Also:
( x°y)°z= x°(y°z)
4. Die Gruppe ist bezüglich der Verknüpfung abgeschlossen
(5. Bei der Verknüpfung gilt das Kommutativgesetz. Also:
x°y= y=°x
Diese Bedingung wird für eine Gruppe zwar nicht gefordert, deswegen hier in Klammern, wird sie
aber dennoch erfüllt spricht man von einer albelischen Gruppe)
Nun stellt sich einem allerdings die Frage, wie die Gruppen jetzt genau verknüpft werden können. Dazu gibt es einige Beispiele. Häufig wird mit sogenannten binären Operatoren verknüpft. Das heißt man wendet zwei Operatoren hintereinander an. Je nach Art der Operation wird die Gruppe unterschiedlich benannt. Als Beispiel werden wir jetzt auf die Menge {0,1,2,3} den binären Operator, zuerst Addition dann Modulo 4 anwenden.
Das Ganze sieht dann so aus:
| ° | 0 | 1 | 2 | 3 |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
Da alle Bedingungen für eine Gruppe zutreffen handelt es sich jetzt um eine sogenannte additive Gruppe Modulo 3.
Führen wir dasselbe mit einer anderen Menge durch. Da wir diesmal eine Multiplikation mit anschließender Modulorechnung durchführen möchten, schließen wir die 0 aus um Bedingung 2 weiterhin zu erfüllen. Unsere Menge enthält also die Zahlen {1,2,3,4}
Die Gruppe ist in Anbetracht der Bedingungen zulässig und heißt multiplikative Gruppe Modulo 5
Die beiden Beispiele von oben sind albelische Gruppen, da bei Addition und Multiplikation das Kommutativgesetz möglich ist.
Alles in Allem
Mir hat die Woche am IWR gut gefallen. Man lernt hier vor allem das selbstorganisierte Arbeiten und hat die Möglichkeit sich mit mathematischen Themen zu beschäftigen, die weit über die normale Schulmathematik hinausgehen. Das Arbeiten an seinem eigenen Thema hat mir hier am meisten Spaß gemacht.